哈夫曼树
哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树,常用于数据压缩中的哈夫曼编码。
基本概念
路径: 在树中,从一个节点到另一个节点之间的分支序列称为路径。
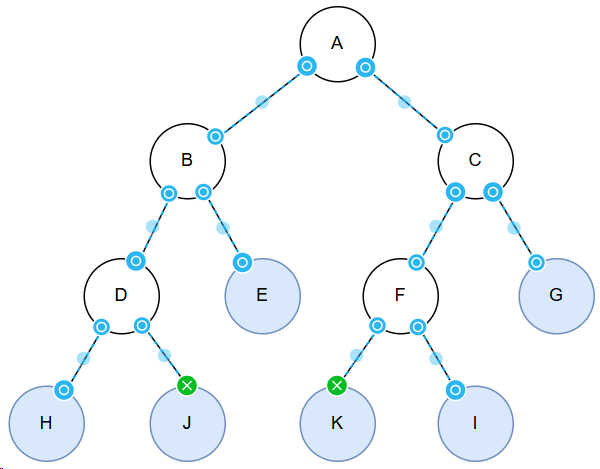
图 1.0
节点的权: 假设给某个节点赋予一个含有意义的数值,这个值就是节点的权,也称权值;
路径长度: 从根节点到某个节点经过的边的数量就是该节点的路径长度;
带权路径长度: 节点的权值 × 路径长度;
树的带权路径长度(WPL): 树中所有叶子节点的带权路径长度之和。WPL 最小的二叉树称为哈夫曼树。
构建示例
对于字符串 HEJJIKKEEGGG,统计各字符出现次数得到字符集 {H:1, J:1, I:2, K: 2, E:3, G: 3},以出现次数作为权值构建哈夫曼树。
字符权值统计:
| 字符 | 出现次数(权值) |
|---|---|
| H | 1 |
| J | 1 |
| I | 2 |
| K | 2 |
| E | 3 |
| G | 3 |
构建过程:
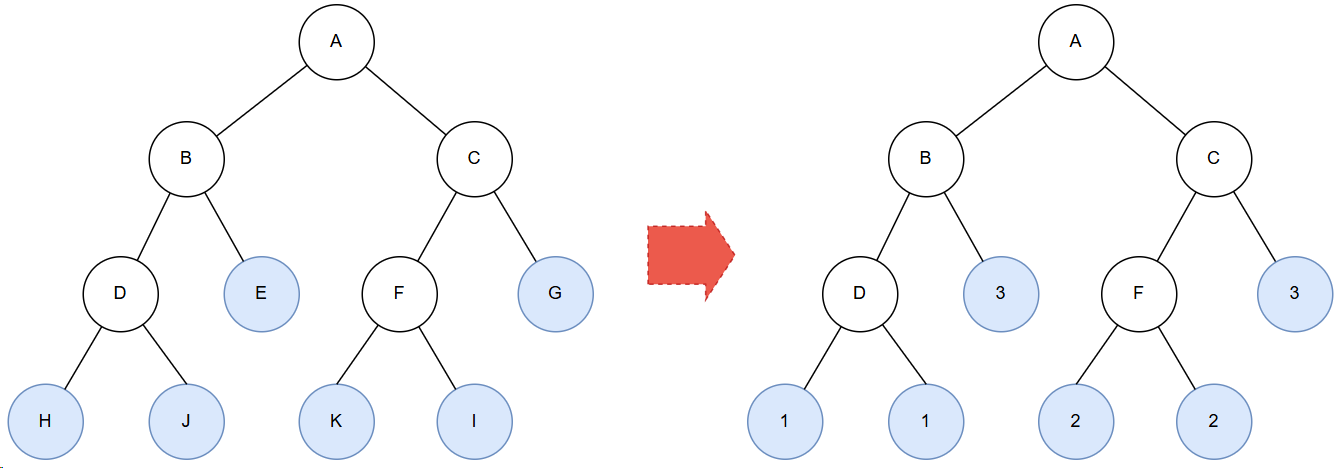
图 1.1 哈夫曼树构建过程
示例说明: 字符 I 的权值为 2,在哈夫曼树中从根节点到 I 的路径长度为 3,则 I 的带权路径长度 = 2 × 3 = 6
字符权值
根据字符集 {H:1, J:1, I:2, K:2, E:3, G:3} 构建哈夫曼树:
| 字符 | 权值 |
|---|---|
| H | 1 |
| J | 1 |
| I | 2 |
| K | 2 |
| E | 3 |
| G | 3 |
叶子节点的带权路径长度
| 节点 | 权值 | 深度 | 带权路径长度 |
|---|---|---|---|
| H | 1 | 3 | 3 |
| J | 1 | 3 | 3 |
| I | 2 | 3 | 6 |
| K | 2 | 3 | 6 |
| E | 3 | 2 | 6 |
| G | 3 | 2 | 6 |
计算结果
WPL = 1×3 + 1×3 + 2×3 + 2×3 + 3×2 + 3×2 = 30
哈夫曼编码
哈夫曼编码是一种前缀编码,采用变长编码方式,常用于数据压缩。
编码规则: 从根节点到叶子节点的路径上,左分支标记为 0,右分支标记为 1,将路径上的所有标记连接起来,即得到该字符的哈夫曼编码。
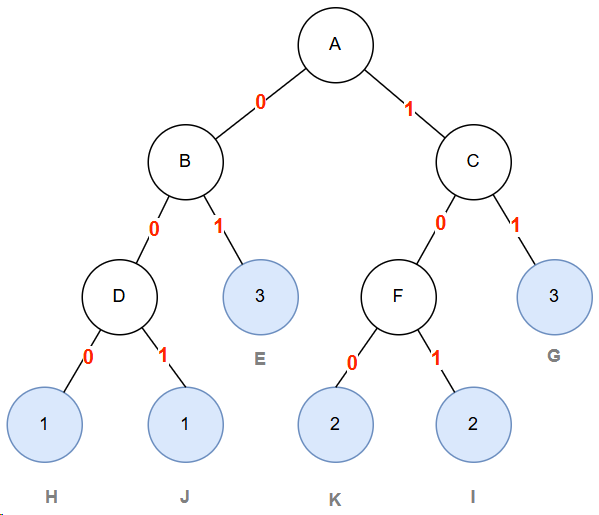
图 1.2 哈夫曼编码树
哈夫曼编码表:
| 字符 | 权值 | 哈夫曼编码 | 码长 |
|---|---|---|---|
| H | 1 | 000 | 3 |
| J | 1 | 001 | 3 |
| E | 3 | 01 | 2 |
| I | 2 | 100 | 3 |
| K | 2 | 101 | 3 |
| G | 3 | 11 | 2 |
- 示例: 根据字符串
HEJJIKKEEGGG,按上表用各字符的哈夫曼编码依次替换,可得出它的哈夫曼编码为:
000 01 001 001 100 101 101 01 01 11 11 11(去掉空格后的最终编码串)
代码实现(Java)
步骤:
- 统计频率
- 构建哈夫曼树
- 生成哈夫曼编码表(可选):生成哈夫曼编码表会占用大量的内存
- 本文在编码和解码过程中采用 树 + 深度优先搜索(DFS)动态生成编码
- 编码
- 解码
// 构建节点对象
public class HuffmanNode implements Comparable<HuffmanNode> {
Character character; // 叶子节点存字符,内部节点为 null
int frequency; // 使用原始类型,避免 Long 装箱
HuffmanNode left;
HuffmanNode right;
public HuffmanNode(Character character, int frequency) {
this.character = character;
this.frequency = frequency;
}
@Override
public String toString() {
return "HuffmanNode{" +
"character=" + character +
", frequency=" + frequency +
'}';
}
@Override
public int compareTo(HuffmanNode o) {
return Integer.compare(this.frequency, o.frequency);
}
}
// frequencyHuffman — 统计字符串中各字符的频率
public static Map<Character, Integer> frequencyHuffman(final String data) {
if (data == null || data.isEmpty()) {
return Map.of();
}
Map<Character, Integer> map = new HashMap<>();
for (char c : data.toCharArray()) {
map.merge(c, 1, Integer::sum);
}
return map;
}
// 构建哈夫曼树
public static HuffmanNode buildHuffmanTree(Map<Character, Integer> frequencyMap) {
PriorityQueue<HuffmanNode> priorityQueue = new PriorityQueue<>();
frequencyMap.forEach((ch, freq) -> priorityQueue.add(new HuffmanNode(ch, freq)));
// 每次取出两个频率最小的节点,合并成一个新节点,直到队列中只剩下一个节点
while (priorityQueue.size() > 1) {
HuffmanNode left = priorityQueue.poll();
HuffmanNode right = priorityQueue.poll();
HuffmanNode parent = new HuffmanNode(null, left.frequency + right.frequency);
parent.left = left;
parent.right = right;
priorityQueue.add(parent);
}
return priorityQueue.poll();
}
// 深度搜索:在哈夫曼树中查找目标字符对应的编码
public static String findCode(HuffmanNode node, char targetChar, String path) {
if (node == null) {
return null;
}
if (node.character != null && node.character == targetChar) {
return path;
}
String leftPath = findCode(node.left, targetChar, path + "0");
if (leftPath != null) {
return leftPath;
}
return findCode(node.right, targetChar, path + "1");
}
// 编码:通过树 + DFS 动态生成编码(不显式保存编码表)
public static String huffmanEncode(String data, HuffmanNode root) {
if (data == null || data.isEmpty() || root == null) {
return "";
}
StringBuilder encodedData = new StringBuilder();
for (char c : data.toCharArray()) {
String code = findCode(root, c, "");
if (code == null) {
throw new IllegalArgumentException("Character not found in Huffman tree: " + c);
}
encodedData.append(code);
}
return encodedData.toString();
}
// 解码:沿哈夫曼树根据 0/1 路径还原原始数据
public static String huffmanDecode(String encodedData, HuffmanNode root) {
if (encodedData == null || encodedData.isEmpty() || root == null) {
return "";
}
StringBuilder decodedData = new StringBuilder();
HuffmanNode current = root;
for (char c : encodedData.toCharArray()) {
if (c == '0') {
current = current.left;
} else if (c == '1') {
current = current.right;
} else {
throw new IllegalArgumentException("Invalid bit in encoded data: " + c);
}
// 到达叶子节点,输出字符
if (current.left == null && current.right == null) {
decodedData.append(current.character);
current = root; // 回到根节点继续解码
}
}
return decodedData.toString();
}
public static void main(String[] args) {
String data = "this is an example for huffman encoding";
Map<Character, Integer> frequencyMap = frequencyHuffman(data);
System.out.println("Character Frequencies: " + frequencyMap);
System.out.println("example: " + data);
HuffmanNode root = buildHuffmanTree(frequencyMap);
System.out.println("Huffman Tree Root Frequency: " + root.frequency);
String encodedData = huffmanEncode(data, root);
System.out.println("Encoded Data: " + encodedData);
String decodedData = huffmanDecode(encodedData, root);
System.out.println("Decoded Data: " + decodedData);
}
最终输出结果
Character Frequencies: { =6, a=3, c=1, d=1, e=3, f=3, g=1, h=2, i=3, l=1, m=2, n=4, o=2, p=1, r=1, s=2, t=1, u=1, x=1}
example: this is an example for huffman encoding
Huffman Tree Root Frequency: 39
Encoded Data: 0000100011100001011111000010111100101111110110011110010100101011100011011111110101011010011100011000011011101010010010111111011011001100101000001100011101010
Decoded Data: this is an example for huffman encoding

评论